How is a tangent different from a chord?

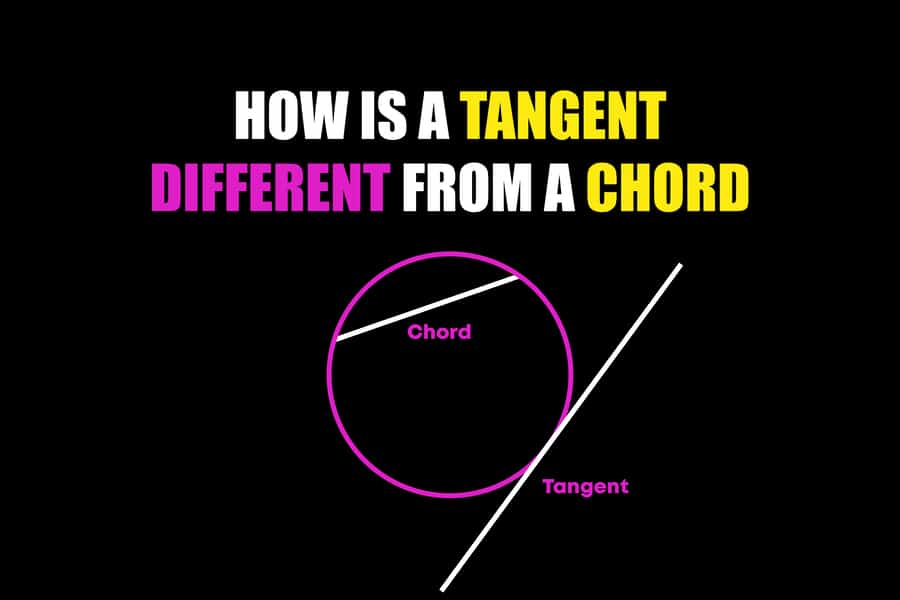
‍Have you ever wondered what the difference is between a tangent and a chord? A tangent and a chord are lines with the same endpoints on a circle. However, the difference between them lies in how they intersect the circle. A chord is a line segment that connects two points on a circle, while a tangent is a line that touches the circle at only one point. A chord will have two points of contact, whereas a tangent will only have one. Additionally, the angle between a tangent and a chord is also different. The angle between a chord and the radius of a circle is always obtuse, while the angle between a tangent and the radius of a circle is always acute. Understanding the differences between a tangent and a chord can help you in your studies of geometry and trigonometry.

How is a tangent different from a chord?

The terms “tangent” and “chord” in geometry are often confused and used interchangeably, but there is a distinct difference between them. A tangent is a line that touches a circle at only one point and is always perpendicular to the circle’s radius at that point. This means that the tangent never crosses the circle and only touches it at one point. 

How are tangents and chords different?

1. A chord connects two points on a circle, while a tangent only touches the circle at one point.
2. The angle between a chord and the radius of a circle is always obtuse, while the angle between a tangent and the radius of a circle is always acute.
3. Understanding the differences between tangents and chords can help you in your studies of geometry and trigonometry.
4. Chords are lines that intersect the circle at two points, while tangents are lines that touch the circle at only one point.
5. The angle between a chord and the radius of a circle is always obtuse, while the angle between a tangent and the radius of a circle is always acute.
6. Chords are more complex than tangents because they have two points of intersection.
7. Tangents are simpler than chords because they only have one point of intersection.

The angle between a tangent and a chord

– is always acute if the tangent is drawn to the circle at a point that is closer to the center of the circle than the chord

– is always obtuse if the tangent is drawn to the circle at a point that is further from the center of the circle than the chord

– is always the same as the angle between the chord and the radius of the circle

– is always less than 90 degrees

– is always perpendicular to the chord

– is always drawn between two points on the circle that is closer to the center of the circle than the chord

– is always drawn between two points on the circle that are further from the center of the circle than the chord.

Applications of tangents and chords

-Chords are used to create shapes on a canvas, such as circles and squares.

-Tangents are used in calculus to find the slope of a line.

-Chords can also be used to measure the distance between two points on a graph.

-Tangents can also be used to find the points of intersection between lines and circles.

-Chords can also be used to find the points of intersection between lines and planes.

-Tangents can also be used to find the points of intersection between lines and solid shapes.

-Chords can also be used to find the points of intersection between lines and surfaces.

-Tangents can also be used to find the points of intersection between lines and curves.

Applications of Tangent and Chord

1. A tangent is used to find the points of intersection of two curves.
2. A chord can be used to create a line between two points on a curve.
3. The angle between a chord and the radius of a circle is always obtuse, while the angle between a tangent and the radius of a circle is always acute.
4. A chord can also be used to create a line between two points on a surface.
5. The angle between a chord and the surface can be found using the Law of Cosines.
6. The angle between a tangent and a surface can be found using the Law of Sines.
7. The angle between a chord and a line can also be found using the Law of Tangents.
8. The angle between a tangent and a point can be found using the Law of Cosines or the Law of Sines.
9. The angle between a chord and a line can also be found using the Law of Triangles.

How are tangents and chords similar?

1. They both have the same endpoint on a circle.
2. The angle between them is always the same.
3. Chords connect two points on the circle, while tangents only touch the circle at one point.
4. The angle between a chord and the radius is always obtuse, while the angle between a tangent and the radius is always acute.
5. Understanding the differences between tangents and chords can help you in your studies of geometry and trigonometry.

Conclusion

If you have ever wondered what the difference is between a tangent and a chord, then hopefully, this article has been helpful. A tangent is a line that touches a curve at only one point, while a chord is a line that connects two points on a circle. The angle between a tangent and the radius is also different, while the angle between a chord and the radius is always obtuse. Both tangents and chords are lines that have the same endpoints on a circle, but there are other differences as well.

FAQ’s

1. What is the difference between a chord and a tangent?

A chord is a line that connects two points on a circle, while a tangent is a line that only touches the circle at one point. Additionally, the angle between a chord and the radius is always obtuse, while the angle between a tangent and the radius is always acute.

2. What is the difference between a tangent and a chord regarding angles?

The angle between a chord and the radius is always obtuse, while the angle between a tangent and the radius is always acute.

3. When is the angle between a chord and the radius always obtuse?

When the chord connects two points that are not on the same diameter of the circle.